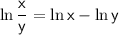Answer:
Statement 1 : False
Statements 2: True
Statements 3: True
Explanation:
Let's evaluate each statement:
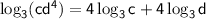
- False: The correct formula is:
 , not
, not
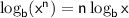
![\sf (3)/(4)(\ln a + \ln b) = \ln \sqrt[4]{a^3b^3}](https://img.qammunity.org/2024/formulas/mathematics/high-school/cgbxi874gpc8puah6s14n14u28l9p2m136.png)
- True: This statement is correct. We can use the fact that:
 .
.
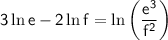
- True: This statement is correct.
We can use the fact that:
 and
and