Question

Solve the logarithmic equation:

2log(x) = log(2) + log(3x - 4)

a) x = 1
b) x = 2
c) x = 3
d) x = 4

Answer 1

To solve the logarithmic equation 2log(x) = log(2) + log(3x - 4), we need to simplify the equation using logarithmic properties and then solve for x. The solutions to the equation are x = 4 and x = 2.

Step-by-step explanation:

To solve the logarithmic equation 2log(x) = log(2) + log(3x - 4), we need to simplify the equation using logarithmic properties and then solve for x.

1. Using the property that log(a) + log(b) = log(a * b), we can rewrite the equation as
   `log(x^2) = log(2) + log(3x - 4).`
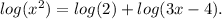
2. Next, using the property that
   `log(a^b) = b * log(a)`, we can simplify further as 2log(x) = log(2 * (3x - 4)).
3. Now we can equate the arguments of the logarithms, so we have x^2 = 2 * (3x - 4).
4. Simplifying the equation, we have
   `x^2 = 6x - 8.`
5. Moving all terms to one side, we get
   `x^2 - 6x + 8 = 0.`
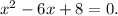
6. Factoring the quadratic equation, we have (x - 4)(x - 2) = 0.
7. Setting each factor equal to 0, we get x - 4 = 0 or x - 2 = 0.
8. Solving for x, we find x = 4 or x = 2.

Therefore, the solutions to the equation are x = 4 and x = 2. The answer is option d) x = 4.