Final answer:
To find intervals where
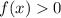 using a
using a
 , you graph the function and use the calculator's graphing tools rather than the ZInterval or TInterval which are for statistical confidence intervals. For functions such as a constant value or those needing sign change analysis, the 'Calc' function helps to identify where the function is positive.
, you graph the function and use the calculator's graphing tools rather than the ZInterval or TInterval which are for statistical confidence intervals. For functions such as a constant value or those needing sign change analysis, the 'Calc' function helps to identify where the function is positive.
Step-by-step explanation:
To find the interval where a function
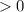 using a
using a
 calculator, we don't typically use the ZInterval or TInterval functions as these are specifically for confidence intervals related to statistics. Instead, when dealing with a function
calculator, we don't typically use the ZInterval or TInterval functions as these are specifically for confidence intervals related to statistics. Instead, when dealing with a function
 , we would graph the function and then use the calculator's capability to determine where on the x-axis the function's value is greater than zero.
, we would graph the function and then use the calculator's capability to determine where on the x-axis the function's value is greater than zero.
For example, if we consider a simple function
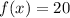 for x ranging from
for x ranging from
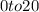 , we can immediately conclude that for all x in this range,
, we can immediately conclude that for all x in this range,
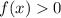 since it is a constant positive function. If the function's graph is more complex, we can use the 'Calc' function on the graph screen to find the zeros of the function, and then determine the intervals based on the sign changes around these zeros.
since it is a constant positive function. If the function's graph is more complex, we can use the 'Calc' function on the graph screen to find the zeros of the function, and then determine the intervals based on the sign changes around these zeros.
For probability calculations involving Student's t-distribution, we use the tcdf function to find the probability within a certain range. If we need to find an interval for a function involving probabilities, we first use inverse probability functions like invT to find critical values and use these to define our interval. Calculations such as the 95 percent confidence interval for a population proportion use the 1-PropZint function on the calculator.