Question

Given: g(x) =4e ⁻⁵^x⁺¹ and h(x)=log₄ (2x=1) evaluate g (h(1)).

Answer 1

To evaluate g(h(1)), where h(x) = log4(2x + 1), we first calculate h(1) as log4(3) and convert that to natural logarithms. Plugging this into
`g(x) = 4e^(-5x + 1) results in 4e^(-(5*ln(3)/ln(4) + 1)).`

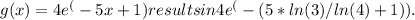
Step-by-step explanation:

To evaluate g(h(1)), we need to first calculate h(1), which is given as h(x) = log4(2x + 1). Since we have h(1), we replace x by 1, and that gives us h(1) = log4(2*1 + 1) = log4(3).

Now, we interpret the value of log4(3) as the power to which 4 must be raised to get 3. However, since our function g(x) requires an input to be plugged into the exponential function, we want to express log4(3) in terms of a natural logarithm. Remembering that we can convert between logarithm bases using the formula logb(a) = ln(a) / ln(b), we have log4(3) = ln(3) / ln(4).

With this conversion, we can now plug this into the function g(x), which is g(x) = 4e-(5x + 1). So, g(log4(3)) turns into g(ln(3)/ln(4)) which is 4e-(5*ln(3)/ln(4) + 1). This can be simplified by calculator or further algebraically.

It is important to note that exponential functions and their inverses, namely logarithms, often require such conversions for simplification.