Question

Find the amplitude of f(x)=4sin(8x+ 5π/6)−2

A. 4
B. 2
C. 6
D. 5/2

Answer 1

The amplitude of the function is
`\( (5)/(2) \)` .

Thus option d is correct.

Step-by-step explanation:

The amplitude of a sine or cosine function represents the maximum displacement from the midline. In the given function
`\( f(x) = 4\sin(8x + (5\pi)/(6)) - 2 \)`, the amplitude is the coefficient of the sine function, which is 4. However, due to the constant term (-2) added at the end, the midline shifts vertically downward by 2 units. To find the actual amplitude from the midline, subtract the constant term from the coefficient of the sine function:
`\( 4 - 2 = (5)/(2) \)`, which is the amplitude.

The amplitude of a sinusoidal function is determined by the coefficient of the sine or cosine term. In this case, the coefficient of the sine function is 4. However, there's a vertical shift represented by the constant term (-2) in the function. This constant shift alters the midline of the graph. The actual amplitude is obtained by considering the difference between the coefficient of the sine term and the constant term, which gives us
`\( 4 - 2 = (5)/(2) \).`

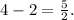
Therefore, the amplitude of the given function
`\( f(x) = 4\sin(8x + (5\pi)/(6)) - 2 \) is \( (5)/(2) \)` units. This value signifies the maximum displacement from the shifted midline of the sinusoidal curve.

Therefore option d is correct.