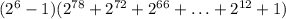Final Answer:
The complete factorization of
 is given by option C)
is given by option C)
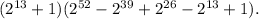
Therefore, correct option is C)
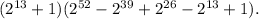
Step-by-step explanation:
Option C) provides the correct factorization of
 . To understand this, we can factor out a common factor of
. To understand this, we can factor out a common factor of
 from the expression, resulting in
from the expression, resulting in
 .
.
Recognizing that
 is a difference of cubes, it can be further factored as
is a difference of cubes, it can be further factored as
 . Thus, the complete factorization becomes
. Thus, the complete factorization becomes
 , which aligns with option C).
, which aligns with option C).
Understanding the properties of exponents and factoring can simplify complex expressions, making it easier to identify correct factorizations. In this case, recognizing the difference of cubes and factoring out common terms helped unveil the correct expression.
Therefore, correct option is C)
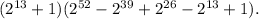
Your question is incomplete, but most probably your full question was
Which among the following expressions provides the complete factorization of
 ?
?
A)
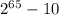
B)

C)

D)