The drawing of the triangle ABC, created with MS Excel is attached
The possible coordinates for points A and B in triangle ΔABC are;
A( -1 , -18 )
B( -1 , 2.8 )
The triangle ABC is constructed using the following steps
The parameters of the triangle ABC are presented as follows;
Segment AB is a vertical line
Angle C is a right angle, therefore, the measure of the angle C, m∠C = 90°
The point C is located at (3, 2)
The slope of the segment AC is 5
The triangle ABC is a right triangle, and the right angle at point C indicates that AC and BC are perpendicular segments
The slope of the segment AC = 5, therefore that the slope of the segment BC can be found using the equation for the relationship between the slope of perpendicular segments, to get;
The slope of BC = -1/5
Taking the point C as being on the right of AB, we get the following coordinate points on AC and BC as follows;
x y-value points on AC y-value points on BC
-1 -18 2.8
0 -13 2.6
1 -8 2.4
2 -3 2.2
3 2 2
The segment AB can be constructed from a selected x-value
The coordinates of the points A and B on the segment AB obtained from the above table of values are; A(-1, -18), B(-1, 2,8)
Please find attached the drawing of the possible triangle ABC, created with MS Excel
The complete question obtained from a similar question found through search can be presented as follows;
Triangle ABC with the following characteristics, is placed on the coordinate plane
 is on a vertical line.
is on a vertical line.
- Point C is located at (3, 2)
- The slope of
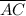 is 5
is 5
What are the possible coordinates of point A and B?
A(___, ___)
B(___, ___)