Question

Use a derivative of function calculator with limit.

a) Find the derivative of f(x) = 3x^3 using the limit
b) Determine the slope of the tangent line to g(x) = e^x at x = 1
c) Calculate the instantaneous rate of change of h(x) = ln(x) at x = 2
d) Find the derivative of k(x) = cos(x) using the limit definition

Answer 1

Final Answers:

a)
`\(f'(x) = \lim_(h \to 0) (f(x + h) - f(x))/(h) = 9x^2\)`

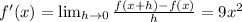
b) The slope of the tangent line to
`\(g(x) = e^x\) at \(x = 1\) is \(e\)` .

c) The instantaneous rate of change of
`\(h(x) = \ln(x)\) at \(x = 2\) is \(1/2\)` .

`d) \(k'(x) = \lim_(h \to 0) (k(x + h) - k(x))/(h) = -\sin(x)\)`

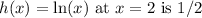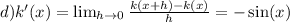
Step-by-step explanation:

a) To find the derivative of
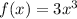`\(f(x) = 3x^3\)` using the limit definition, we apply

the formula for the derivative:
`\(f'(x) = \lim_(h \to 0) (f(x + h) - f(x))/(h)\)` . For
`\(f(x) = 3x^3\)` ,

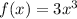applying the limit definition gives us
`\(f'(x) = \lim_(h \to 0) (3(x + h)^3 - 3x^3)/(h)\)` ,

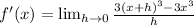simplifying this yields
`\(f'(x) = 9x^2\)` .

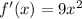b) The slope of the tangent line to
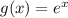`\(g(x) = e^x\)` at
`\(x = 1\)` can be found by

evaluating the derivative of
`\(g(x)\)` at that point. The derivative of
`\(e^x\)` is

itself, so
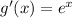`\(g'(x) = e^x\)` . At
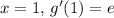`\(x = 1\), \(g'(1) = e\)` , indicating the slope of the

tangent line.

c) To determine the instantaneous rate of change of
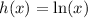`\(h(x) = \ln(x)\)` at

`\(x = 2\)` , we find its derivative. The derivative of
`\(\ln(x)\)` is
`\(1/x\)` . So, at
`\(x = 2\)` ,

the derivative
`\(h'(2) = 1/2\)` represents the instantaneous rate of change.

d) For
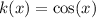`\(k(x) = \cos(x)\)` , using the limit definition of the derivative,
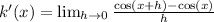`\(k'(x) = \lim_(h \to 0) (\cos(x + h) - \cos(x))/(h)\)` . Simplifying this limit

expression results in
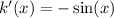`\(k'(x) = -\sin(x)\)` , giving us the derivative of
`\(\cos(x)\)`.