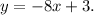The equation in slope-intercept form of the line that passes through
 and is parallel to the graph of
and is parallel to the graph of
 is
is
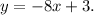
The equation of a line in slope-intercept form is given by
 , where \(m\) is the slope and \(b\) is the y-intercept.
, where \(m\) is the slope and \(b\) is the y-intercept.
For a line parallel to the given line \(y = -8x - 2\), the slopes of the two lines are the same. Therefore, the slope (\(m\)) of the new line is also -8.
Now, we can use the point-slope form of the equation of a line, which is
 where
where
 is a point on the line and
is a point on the line and
 is the slope.
is the slope.
Given the point
 and the slope
and the slope
 , substitute these values into the point-slope form:
, substitute these values into the point-slope form:
![\[y - 11 = -8(x - (-1))\]](https://img.qammunity.org/2024/formulas/mathematics/college/o66wf4ytpcaxag05f09p2do4yvjs6sz89w.png)
Simplify the equation:
![\[y - 11 = -8(x + 1)\]](https://img.qammunity.org/2024/formulas/mathematics/college/eciupyou13v45qcylf0idvlsv0k8d9hmei.png)
Distribute the -8:
![\[y - 11 = -8x - 8\]](https://img.qammunity.org/2024/formulas/mathematics/college/x88wjyzjos408c8kpstgwjxfin31e4zstb.png)
Now, isolate \(y\) by adding 11 to both sides of the equation:
![\[y = -8x - 8 + 11\]](https://img.qammunity.org/2024/formulas/mathematics/college/ry5xvilxm2oldcy0lg6oi387ivugdutmoh.png)
Combine the constants:
![\[y = -8x + 3\]](https://img.qammunity.org/2024/formulas/mathematics/college/qy3vpnqtbdlbb70j3k6r2hpmjazn0nay18.png)
So, the equation in slope-intercept form of the line that passes through
 and is parallel to the graph of \
and is parallel to the graph of \
 ) is
) is