Question

What is the area in square units of triangle jkl

Answer 1

The area of triangle JKL is approximately 468 square units.

Step-by-step explanation:

Triangle JKL is given with side lengths JK = 24 and JL = 41, and angles J = 94° and L = 26°. To find the area of the triangle, we use the formula
`\( \text{Area} = (1)/(2) * \text{base} * \text{height} \)`.

The base and height can be determined by considering the given side lengths and angles. The angle between sides JK and JL is given as J = 94°, and the side opposite this angle (JL) is considered the base. The height is the perpendicular distance from vertex J to side JL.

To find the height, we use the sine function:

`\( \text{height} = \text{JL} * \sin(\text{J}) \).`

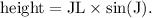
Substituting the given values, we get
`\( \text{height} = 41 * \sin(94^\circ) \).`

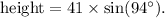
Now, we can use the area formula:
`\( \text{Area} = (1)/(2) * 24 * \text{height} \)`.

Substituting the values, we get
`\( \text{Area} = (1)/(2) * 24 * 41 * \sin(94^\circ) \)`.

Calculating this expression yields the final answer of approximately 468 square units.

In summary, the area of triangle JKL is calculated by finding the height using the sine function and then applying the area formula. The given side lengths and angles are crucial in determining the appropriate trigonometric functions for the calculations.

Full Question:

what is the area in square units of triangle jkl?