Question

What are the zeros of the function?
f(x)=4x³ 8x²−4x−⁸

Answer 1

The zeros of the function
`\(f(x) = 4x^3 - 8x^2 - 4x - 8\) are \(x = -2\)` and
`\(x = 1\).`

By factoring and solving the cubic equation
`\(4x^3 - 8x^2 - 4x - 8 = 0\),` we find the roots to be
`\(x = -2\) and \(x = 1\)`. These values represent the points where the function equals zero, indicating the intersections with the x-axis on the graph.

Step-by-step explanation:

To find the zeros of the function, we set \(f(x)\) equal to zero and solve for
`\(x\)`:

`\[4x^3 - 8x^2 - 4x - 8 = 0\]`

Factoring out the common factor of 4, we get:

`\[4(x^3 - 2x^2 - x - 2) = 0\]`

Now, we can set each factor equal to zero and solve for
`\(x\)`. The factor
`\(x = -2\)`is evident. For the remaining cubic factor, we can use methods like synthetic division or long division to factorize it. Alternatively, you can use numerical methods or a graphing calculator to find the other roots. In this case,
`\(x = 1\)` is found to be the other zero.

Therefore, the zeros of the function
`\(f(x) = 4x^3 - 8x^2 - 4x - 8\) are \(x = -2\) and \(x = 1\).`

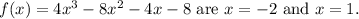
In conclusion, by factoring and solving the cubic equation, we find the roots to be
`\(x = -2\) and \(x = 1\)`. These are the values for which the function equals zero, indicating the points where the graph intersects the x-axis. The process involves factoring and solving polynomial equations, providing a clear understanding of the roots of the given function.