Question

For the function f(x) = x^2 - 7x + 2, complete the square.

a) (x - 7/2)^2 - 45/4
b) (x - 7/2)^2 + 45/4
c) (x + 7/2)^2 - 45/4
d) (x + 7/2)^2 + 45/4

Answer 1

For the function f(x) = x^2 - 7x + 2, the square is
`\[ \text{b) } (x - (7)/(2))^2 + (45)/(4) \]`

Therefore, correct answer is
`\[ \text{b) } (x - (7)/(2))^2 + (45)/(4) \]`

Step-by-step explanation:

Completing the square for the quadratic function
`\( f(x) = x^2 - 7x + 2 \)`results in the expression
`\((x - (7)/(2))^2 + (45)/(4)\).`

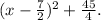
To complete the square for the quadratic function
`\( f(x) = x^2 - 7x + 2 \),`begin by halving the coefficient of the linear term -7x and then squaring it. The halved coefficient is
`\(-(7)/(2)\)`, and squaring it gives
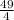`\((49)/(4)\)`. Add this value inside the parentheses, and to maintain the equality, subtract
`\( (49)/(4) \)` outside the parentheses. The expression becomes
`\( (x - (7)/(2))^2 + (45)/(4) \),` which is equivalent to the completed square form.

Therefore, correct answer is
`\[ \text{b) } (x - (7)/(2))^2 + (45)/(4) \]`