Question

Consider the matrix equation below taken from a linear system of equations. Using Cramer's Rule, select the correct ratio of determinants to determine the correct value for x.

Answer 1

The determinant that represents the value of x is (a)
`x= \frac{\left[\begin{array}{cc}1&2&-3&4\end{array}\right]}{\left[\begin{array}{cc}-3&2&5&4\end{array}\right]}`

Solving the linear system of equations using Cramer's Rule

From the question, we have the following parameters that can be used in our computation:

`\left[\begin{array}{cc}1&2&-3&4\end{array}\right] \left[\begin{array}{c}x&y\end{array}\right] = \left[\begin{array}{c}-3&5\end{array}\right]`

To calculate x, we start by calculating the derivative of the matrix

So, we have:

`\delta = \left[\begin{array}{cc}1&2&-3&4\end{array}\right]`

Next, we have

`\delta_x = \left[\begin{array}{cc}-3&2&5&4\end{array}\right]`

The value of x is then calculated as

`x = (\delta x)/(\delta)`

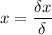
Substitute the known values into the equation

`x= \frac{\left[\begin{array}{cc}1&2&-3&4\end{array}\right]}{\left[\begin{array}{cc}-3&2&5&4\end{array}\right]}`

Hence, the value of x is (a)
`x= \frac{\left[\begin{array}{cc}1&2&-3&4\end{array}\right]}{\left[\begin{array}{cc}-3&2&5&4\end{array}\right]}`