The determinant that represents the value of x is (a)
![x= \frac{\left[\begin{array}{cc}1&2&-3&4\end{array}\right]}{\left[\begin{array}{cc}-3&2&5&4\end{array}\right]}](https://img.qammunity.org/2024/formulas/mathematics/college/3xft33l7nnmeuq6a0nec9mcc5hxq308pbs.png)
Solving the linear system of equations using Cramer's Rule
From the question, we have the following parameters that can be used in our computation:
![\left[\begin{array}{cc}1&2&-3&4\end{array}\right] \left[\begin{array}{c}x&y\end{array}\right] = \left[\begin{array}{c}-3&5\end{array}\right]](https://img.qammunity.org/2024/formulas/mathematics/college/i8fxyhgkpl1mwa6x844nghdgm0tnf1n3u4.png)
To calculate x, we start by calculating the derivative of the matrix
So, we have:
![\delta = \left[\begin{array}{cc}1&2&-3&4\end{array}\right]](https://img.qammunity.org/2024/formulas/mathematics/college/nfsuuil693os2fb2oul63xeath4rxmq67b.png)
Next, we have
![\delta_x = \left[\begin{array}{cc}-3&2&5&4\end{array}\right]](https://img.qammunity.org/2024/formulas/mathematics/college/oixkhmze7sob9ao21zxyije2cybdihf23x.png)
The value of x is then calculated as
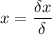
Substitute the known values into the equation
![x= \frac{\left[\begin{array}{cc}1&2&-3&4\end{array}\right]}{\left[\begin{array}{cc}-3&2&5&4\end{array}\right]}](https://img.qammunity.org/2024/formulas/mathematics/college/3xft33l7nnmeuq6a0nec9mcc5hxq308pbs.png)
Hence, the value of x is (a)
![x= \frac{\left[\begin{array}{cc}1&2&-3&4\end{array}\right]}{\left[\begin{array}{cc}-3&2&5&4\end{array}\right]}](https://img.qammunity.org/2024/formulas/mathematics/college/3xft33l7nnmeuq6a0nec9mcc5hxq308pbs.png)