Question

Create a two column proof: 4.

Given: AC = ED, B is the midpoint of AC
<BED <BDE, <ABE = <CBD
Prove: ACDE is a parallelogram​

Answer 1

The figure shows a quadrilateral ACDE with a line segment BD intersecting at point B, which is the midpoint of line segment AC. There are angle markings indicating that angles BED and BDE are congruent, as well as angles ABE and CBD.

Therefore ACDE is a parallelogram.

The image contains a geometric figure with a set of given conditions and a statement to prove. Here are the details:

Given:

`\overline{AC} \cong \overline{ED}` $$

B is the midpoint of
`\overline{AC}`

`\angle BED \cong \angle BDE` $$

`\angle ABE \cong \angle CBD` $$

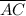
Prove:

A parallelogram is a four-sided polygon (a flat, closed figure with straight sides) in which opposite sides are parallel and of equal length. This means that the opposite sides of a parallelogram never intersect and are always of the same length. Additionally, opposite angles in a parallelogram are equal, and the sum of adjacent angles is always 180 degrees.

- Quadrilateral ACDE is a parallelogram.

- Triangle ABE is congruent to Triangle CBD.

The figure shows a quadrilateral ACDE with a line segment BD intersecting at point B, which is the midpoint of line segment AC. There are angle markings indicating that angles BED and BDE are congruent, as well as angles ABE and CBD.

Therefore ACDE is a parallelogram.