Question

A boy throws a stone straight upward with an initial speed of 15 m/s on the surface of the earth. What maximum height above the starting point will the stone reach before falling back down?

Answer 1

The stone will reach a maximum height of 11.59 meters above the starting point before falling back down.

Step-by-step explanation:

The maximum height above the starting point that the stone will reach before falling back down can be calculated using the equations of motion. Since the stone is thrown straight upward, the initial velocity is positive and the acceleration due to gravity is negative. First, we can calculate the time it takes for the stone to reach its maximum height:

Using the equation v = u + at, where v is the final velocity (which will be 0 at the maximum height), u is the initial velocity (15 m/s), a is the acceleration (-9.8 m/
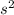`s^(2)`)and t is the time, we can rearrange the equation to solve for t:

0 = 15 - 9.8t

9.8t = 15

t = 15/9.8

t = 1.53 seconds

The time it takes for the stone to reach its maximum height is 1.53 seconds. Next, we can calculate the maximum height using the equation:

s = ut + 1/2
`at^(2)`

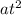
s = 15*1.53 + (1/2)(-9.8)
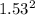`1.53^(2)`s = 22.95 - 11.36

s = 11.59 meters

The stone will reach a maximum height of 11.59 meters above the starting point before falling back down.