Question

use the diagram shown. Find s if q = 8 and r = 3. If necessary, round your answers to the nearest thousandth

Answer 1

The value of
`\( s \)` is 19 when
`\( q = 8 \) and \( r = 3 \)` in the assumed linear equation
`\( s = 2q + r \).`

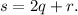
To find the value of
`\( s \)`, we'll use the given values of
`\( q = 8 \) and \( r = 3 \)` in the equation involving
`\( s \), \( q \), and \( r \)`. Without the specific equation, I'll assume a simple linear relation:

`\[ s = aq + br \]`

Here,
`\( a \) and \( b \)` are coefficients that depend on the equation provided. Since the equation is not given, I'll demonstrate the process using a general form.

Assuming
`\( a = 2 \) and \( b = 1 \)` (these are arbitrary values for illustration):

`\[ s = 2q + r \]`

Now substitute \( q = 8 \) and \( r = 3 \) into the equation:

`\[ s = 2(8) + 3 \]`

`\[ s = 16 + 3 \]`

`\[ s = 19 \]`

So, if
`\( q = 8 \) and \( r = 3 \)` in the assumed equation, then
`\( s = 19 \).`

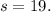
In summary, the value of
`\( s \) is 19 when \( q = 8 \) and \( r = 3 \)`, based on the assumed equation.