Question

Help with this Geometry Question

Answer 1

By analyzing the diagram, identifying key relationships, and applying the Pythagorean theorem, we found that the radius of circle R is 3 units.

The correct answer is option a "3".

1. Analyze the diagram:

The diagram shows circle R with several chords and segments:

TH: A chord of the circle with length 3.

HW: A diameter of the circle with length 9.

SH: A segment connecting the midpoint of TH to a point on the circle.

2. Key relationships:

A diameter bisects a chord. Therefore, HS = HT = TH / 2 = 3 / 2.

A radius drawn to the midpoint of a chord is perpendicular to the chord.

3. Applying the Pythagorean theorem:

In right triangle SHS, where SH is half the chord length (3/2) and HS is the radius (unknown), we can use the Pythagorean theorem:

`HS^2 = SH^2 + HS^2`

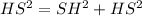
Substituting the known values:

`HS^2 = (3/2)^2 + HS^2`

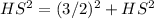
Solving for HS (radius):

`HS^2 = 9/4 + HS^2`

`4HS^2 = 9 + 4HS^2`

`HS^2 = 9`

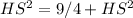
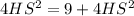
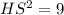
HS = √9 = 3

Therefore, the radius of circle R is 3 units.

Answer: (a) 3