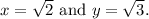Final Answer:
The solution to the system of nonlinear equations is
 and
and
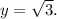
Step-by-step explanation:
To solve the system of equations
 and \(xy = 2\), we can use substitution. First, express one of the variables in terms of the other using the second equation. Solving for \(y\), we get
and \(xy = 2\), we can use substitution. First, express one of the variables in terms of the other using the second equation. Solving for \(y\), we get
 Substitute this expression for \(y\) into the first equation:
Substitute this expression for \(y\) into the first equation:
![\[x^2 + \left((2)/(x)\right)^2 = 5.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kd3a9jtxzdx287kqpg73zck0bw9agn29ue.png)
Simplify this equation:
![\[x^2 + (4)/(x^2) = 5.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/l07w54zg4r8jrfp8vvwurwbcsy2tn0bvoh.png)
Multiply through by
 to get rid of the fraction:
to get rid of the fraction:
![\[x^4 + 4 = 5x^2.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9y66uvy15rtefw9shjkjos9927srz5kyf3.png)
Rearrange to form a quadratic equation:
![\[x^4 - 5x^2 + 4 = 0.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y1bmd2pgxp9lj6c1vhp6l5snpieahnet0r.png)
Factor this equation:
![\[(x^2 - 1)(x^2 - 4) = 0.\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/mncl0zsyleb9bi7jphr90pn0q7wgmd3ocx.png)
This yields two possible values for \(x\): \(x = 1\) or \(x = -1\) from the first factor, and \(x = 2\) or \(x = -2\) from the second factor. However, considering the positive solutions, we have \(x = 1\) or
 Substitute these back into the second equation \(xy = 2\) to find the corresponding values of \(y\). The solution
Substitute these back into the second equation \(xy = 2\) to find the corresponding values of \(y\). The solution
 satisfies both equations. Therefore, the final answer is
satisfies both equations. Therefore, the final answer is