Question

If a, equals, minus, 4, x, minus, 4, ia=−4x−4i and b, equals, 3b=3, then find the value of the a, b, cubedab

3
in fully simplified form.

Answer 1

Based on the given expression, the value of
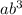`ab^3`, in fully simplified form, is
`-108x - 108i.`

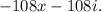
How to solve the expression

To find the value of
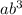`ab^3`, substitute the given values of a and b into the expression and simplify.

Given:

a = -4x - 4i

b = 3

Substitute the values into the expression:

`ab^3 = (-4x - 4i)(3)^3`

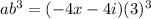
Expand and simplify

`ab^3 = (-4x - 4i)(27)`

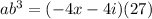
Use the distributive property:

`ab^3 = -4x * 27 - 4i * 27`

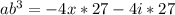
Simplify the multiplication:

`ab^3 = -108x - 108i`

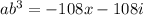
Therefore, the value of
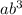`ab^3`, in fully simplified form, is -108x - 108i.