Question

Use the figure to prove that the sum of the interior angies of a triangle equals 180

Given: CD parell to AB
Prove: m<1+m<2+ m<3 = 180°

Answer 1

The statement that the sum of the interior angles of a triangle is equal to 180 degrees is known as the triangle angle sum theorem. The prove is given below.

The statement that the sum of the interior angles of a triangle is equal to 180 degrees is known as the triangle angle sum theorem. There are many ways to prove this theorem, and the one provided uses the concept of parallel lines and corresponding angles.

Here's how the proof goes:

1. Draw a transversal line intersecting line AB and line CD. Let's call the point of intersection E.

2. Identify corresponding angles. Since AB || CD, we have corresponding angles:

`\angle1 \ and\ \angle CED`

`\angle 2\ and\ \angle DEB`

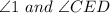
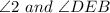
3. Sum the corresponding angles. We get:

`\angle1 + \angle2 + \angle CED + \angle DEB = 180\textdegree` (since the angles on a straight line add up to 180°)

4. Substitute the interior angles of the triangle. Since angle CED and angle DEB are interior angles of the triangle, we can rewrite the equation as:

`\angle1 + \angle2 + \angle CED + \angle DEB = 180\textdegree`

`\angle1 + \angle2 + \angle3 = 180\textdegree`

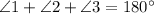
Therefore, the sum of the interior angles of triangle ABE is equal to 180 degrees.

This proof relies on the fact that corresponding angles are equal when two lines are parallel and intersected by a transversal. This is a fundamental property of parallel lines and is crucial for understanding many geometric relationships.