Question

Solve The Differential Equation. y' + 3xeʸ = 0

Answer 1

To solve the differential equation y
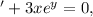`' + 3xe^y = 0,` ables, integrate both sides, and isolate y to find the general solution, which is
`Y = -ln(|1.5x^2 + C|),`.

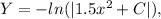Step-by-step explanation:

The differential equation y' + 3xe^y = 0 is separable. Solving it involves rearranging the terms so that each variable and its differential are on opposite sides of the equation. The steps for solving this equation are as follows:

1. Separate the variables by dividing both sides by e^y and then multiplying both sides by dx to get
   `Y = -ln(|1.5x^2 + C|),`
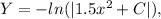
2. Integrate both sides. The left side will integrate to -e^(-y), and the right side will integrate to -
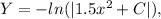   `Y = -ln(|1.5x^2 + C|),`ach side plus a constant of integration, C.
3. Solve for y by taking the natural logarithm if necessary, and then isolating y on one side of the equation.

The general solution to the differential equation will be of the form Y = -ln(|1.5x^2 + C|), where C is the constant of integration.