(a) The table and curve for the function
 have been filled in and plotted.
have been filled in and plotted.
(b) The maximum height of the arch above the ground is 9 feet.
(a) To fill in the table and draw the curve for the function
 , we can substitute each value of x into the equation and calculate the corresponding y.
, we can substitute each value of x into the equation and calculate the corresponding y.
(Given in the attachment)
Now, plotting these points on a graph and connecting them with a smooth curve, we get the shape of the arch.
(Given in the attachment)
(b) To find the maximum height of the arch above the ground, we need to identify the vertex of the parabola, which represents the maximum point. The given function
 is a downward-facing parabola, and its vertex is the maximum point.
is a downward-facing parabola, and its vertex is the maximum point.
The vertex form of the parabola is
 , where
, where
 is the vertex. In this case,
is the vertex. In this case,
 and
and
 , so the vertex is
, so the vertex is
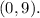
Therefore, the maximum height of the arch above the ground is 9 feet.