Question

Solve triangle ABC if m

Answer 1

The values for the angles and sides of triangle ABC are:

m(A)≈87°

b≈4.958

c≈1.950

To solve the triangle ABC, we can use the Law of Sines, which states:

`(a)/(sin(A)) =(b)/(sin(B)) =(c)/(sin(C))`

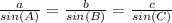
Given that

m(B)=71°, m(C)=22°, and a=5.20, we can find angle A using the fact that the sum of angles in a triangle is 180°:

m(A)=180°−m(B)−m(C)

m(A)=180°−71°−22°

m(A)=87°

Now, we can use the Law of Sines to find the other sides of the triangle:

`(a)/(sin(A)) =(b)/(sin(B)) \\(5.20)/(sin(87)) =(b)/(sin(71))`

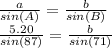
Now, solve for b:

`b= (5.20.sin(71))/(sin(87)) \\b= (5.20-0.951)/(0.996) \\b= 4.958`

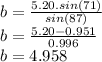
Now, we can find side c using the Law of Sines:

`(c)/(sin(C)) =(a)/(sin(A)) \\\\(c)/(sin(22)) =(b)/(sin(87))`

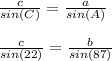
Now, solve for c:

`c= (5.20.sin(22))/(sin(87)) \\c= (5.20-0.374)/(0.996) \\c= 1.950`

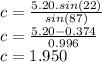
So, the values for the angles and sides of triangle ABC are:

m(A)≈87°

b≈4.958

c≈1.950