Question

Y+1/4x=1x=−1/4x+1 how many solutions

(THE 1/4 ARE FRACTIONS BTW)

Answer 1

The system of equations has one unique solution, which is (x, y) = (1, 1).

This problem involves solving a system of equations with two variables, y and x. The equations given are:

`\(y + (1)/(4)x = 1\)`

`\(x = -(1)/(4)y + 1\)`

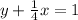
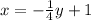
To determine the number of solutions, let's examine the equations. The second equation is already solved for x in terms of y, so we can substitute this expression for x into the first equation:

`\(y + (1)/(4)x = 1\)`

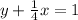
Substitute
`\(x = -(1)/(4)y + 1\):`

`\(y + (1)/(4) \cdot (-(1)/(4)y + 1) = 1\)`

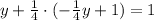
Simplify the equation:

`\(y - (1)/(16)y + (1)/(4) = 1\)`

Combine like terms:

`\((15)/(16)y + (1)/(4) = 1\)`

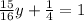
Now, isolate y:

`\((15)/(16)y = 1 - (1)/(4)\)`

`\((15)/(16)y = (3)/(4)\)`

`\(y = (3)/(4) * (16)/(15)\)`

`\(y = 1\)`

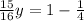
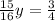
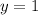
Now that we have found y, let's substitute it back into the second equation to find x:

`\(x = -(1)/(4)y + 1\)`

`\(x = -(1)/(4) * 1 + 1\)`

`\(x = 1\)`

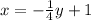
After solving, we find that y = 1 and x = 1. Both equations are satisfied when x = 1 and y = 1. Therefore, the system of equations has one unique solution, which is (x, y) = (1, 1).