Question

If the sum of two numbers is 4 and the sum of their spuares minus three times their product is 76, find the numbers

Answer 1

-2 and 6

Explanation:

Mark the first number as x

and the second number as y

Since x + y = 4

y = 4 - x

// substitute the given value of y into the equation

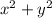`x^(2) + y^(2)` - 3xy = 76

`x^(2)` +
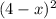`(4-x)^(2)` - 3 * x * (4 - x) = 76

`x^(2)` + 16 - 8x +
`x^(2)` - 12x + 3
`x^(2)` = 76

`x^(2)` +
`x^(2)` + 3
`x^(2)` - 20x = 76 - 16

5
`x^(2)` - 20x = 60

5
`x^(2)` - 20x - 60 = 0

// divide both sides by 5

`x^(2)` - 4x - 12 = 0

// write -4 x as a difference, this way it is faster than calculating discriminant

`x^(2)` + 2x - 6x - 12 = 0

// factor out x and -6 from the expression

x (x +2) - 6 (x +2) = 0

(x - 6) * (x + 2) = 0

// there are two possible cases

1) x - 6 = 0

2) x + 2 = 0

1) x = -2

2) x = 6

// substitute the given value of x into the equation

1) y = 4 - x = 4 - (-2) = 6

2) y = 4 - x = 4 - 6 = -2

Now we get two pairs (-2; 6) and (6; -2), which are the solutions to the system

Since their sequence as the question suggests is irrelevant, the numbers are -2 and 6

Answer 2

`Suppose~that~two~numbers~are~x~and~y.\\From~the~first~condition,\\x+y=4.........(1)\\or, y=4-x.......(2)\\From~the~second~condition,\\x^2+y^2-3xy=76\\or, (x+y)^2-2xy-3xy=76\\or, 4^2-5xy=76\\or, -5xy = 76-16\\or, -5xy = 60\\or, xy = -12\\From~eq^n~(2),\\x(4-x)=-12\\or, 4x-x^2=-12\\or, x^2-4x-12=0\\or, x^2 +2x-6x-12=0\\or, x(x+2)-6(x+2) = 0\\or,(x+2)(x-6) = 0\\i.e. x = -2 ~or ~6\\When~ x=-2, y=4-(-2) = 4+2 =6\\When~x=6, y=4-6 = 4-6 = -2\\So,~the~two~numbers~are~-2~and~6.`