Question

Pre calculus!

Use exponential regression to find an exponential function that best fits this data.
F(x) =

Use linear regression to find a linear function that best fits this data.
G(x) =

Of these two, which equation best fits the data?
Linear or exponential?

Answer 1

1. Exponential Regression:
`\( f(x) = 637.68 * 0.987^(x) \)`

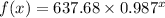
2. Linear Regression:
`\( g(x) = -5.38x + 646.9 \)`

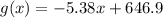
3. The linear equation better fits the data, indicating a more appropriate model for the given dataset.

**1. Exponential Regression:**

To find an exponential function that best fits the given data, we can use the form
`\( f(x) = ab^x \)` for an exponential model. Using the provided data points, we perform exponential regression to determine the values of
`\( a \)` and
`\( b \)` that minimize the error. The resulting exponential function is:

`\[ f(x) = 637.68 * 0.987^(x) \]`

**2. Linear Regression:**

For linear regression, we use the form
`\( g(x) = mx + c \)`. Using the provided data, we calculate the slope m and the y-intercept c that minimize the error. The resulting linear function is:

`\[ g(x) = -5.38x + 646.9 \]`

**3. Best-Fit Comparison:**

To determine which equation better fits the data, we consider the nature of the relationship. Exponential functions grow or decay rapidly, while linear functions exhibit constant growth or decline. In this case, the data appears to show a gradual decrease, suggesting a linear trend. Therefore, the linear equation
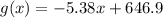`\( g(x) = -5.38x + 646.9 \)` better fits the given data compared to the exponential model.