Question

One positive integer is 4 less than twice another. The sum of their squares is 772 . Find the integers

Answer 1

The positive integers are 21 and 38, where one integer is 4 less than twice the other. The sum of their squares is 772, satisfying the given conditions.

Let's denote the two positive integers as x and y, with x > y. According to the given information:

1. x is 4 less than twice y: x = 2y - 4.

2. The sum of their squares is 772:
`\(x^2 + y^2 = 772\).`

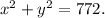
Now, substitute the expression for x from the first equation into the second:

`\[(2y - 4)^2 + y^2 = 772\]`

Expand and simplify:

`\[4y^2 - 16y + 16 + y^2 = 772\]`

Combine like terms:

`\[5y^2 - 16y + 16 = 772\]`

Subtract 772 from both sides:

`\[5y^2 - 16y - 756 = 0\]`

Factor the quadratic equation:

(5y + 36)(y - 21) = 0

This gives two possible solutions for y:
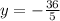`\(y = -(36)/(5)\)` (extraneous) or y = 21.

Substitute y = 21 back into the first equation to find x:

x = 2(21) - 4 = 38

Therefore, the two positive integers are 21 and 38.