Answer:
we have two equations:
2*x + y = 20
y = a + 18/x - 3
We want to find the values of a such that the graphs of the equations do not intersect.
The first step is to isolate y in the first equation.
now we get:
y = 20 - 2*x
Then we have the system of equations:
y = 20 - 2*x
y = a + 18/x - 3
If the line intersects the curve at a point (x, y), then at that point both functions have the same value of y, then:
20 - 2*x = y = a + 18/x- 3
We want to find a value of such that this does not happen.
Let's solve that equation and see what we can find.
20 - 2*x = a + 18/x - 3
20 + 3 = a + 18/x + 2*x
23 = a + 18/x + 2*x
(23 - a) = 18/x + 2*x
if we multiply all values by x, we get:
(23 - a)*x = 18 + 2*x^2
Then we have a quadratic equation, we can write this as:
2*x^2 - (23 - a)*x + 18 = 0
Now, remember that if the determinant of the quadratic function is smaller than zero, then the function does not have any real solution, then we need to find a such that the determinant of this quadratic equation is smaller than zero.
Remember that for a quadratic equation:
a*x^2 + b*x + c = 0 is:
b^2 - 4*a*c
In this case, the determinant is:
(-(23 - a))^2 - 4*2*18
(23 - a)^2 - 144
And this must be smaller than zero, then:
(23 - a)^2 - 144 < 0
23^2 - 2*23*a + a^2 - 144 < 0
529 - 46*a + a^2 - 144 < 0
a^2 - 46*a + 385 < 0
Notice that the function has a positive leading coefficient, then the arms of the function go upwards, then the region of the function that is smaller than zero is the values of a that are between both roots of a.
Then we need to solve:
a^2 - 46*a + 385 = 0
We can use the Bhaskara's equation to find the roots, the roots are given by:
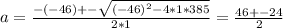
Then the two roots are:
a₁ = (46 + 24)/2 = 35
a₂ = (46 - 24)/2 = 11
Then for all the values of a suc that:
11 < a < 35
The line does not intersect the curve.