1 Answer

Rec · Answer 1 · 2024-01-24T08:07:46+0000

Answer:

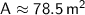
$\sf A \approx 78.5 \, \textsf{m}^2$

Explanation:

The formula for the area (
$\sf A$ ) of a circle is given by:

$\sf A = \pi r^2$

where
$\sf r$ is the radius of the circle. The radius is half of the diameter, so
$\sf r = (d)/(2)$ , where
$\sf d$ is the diameter.

Given that the diameter (
$\sf d$ ) is 10 m, we can find the radius (
$\sf r$ ):

$\sf r = (d)/(2) = \frac{10 \, \textsf{m}}{2} = 5 \, \textsf{m}$

Now, we can substitute the radius into the formula for the area:

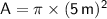
$\sf A = \pi * (5 \, \textsf{m})^2$

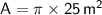
$\sf A = \pi * 25 \, \textsf{m}^2$

Using the approximate value of
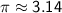$\sf \pi \approx 3.14$ , we can calculate the area:

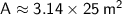
$\sf A \approx 3.14 * 25 \, \textsf{m}^2$

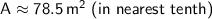
$\sf A \approx 78.5 \, \textsf{m}^2 \textsf{ (in nearest tenth)}$

Therefore, the area of the circle is approximately
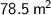$\sf 78.5 \, \textsf{m}^2$ to the nearest tenth.

Please log in or register to add a comment.