Question

The relationship between the elapsed time t, in months, since Venera sent the letter, and the number of

people, P(t), who receive the email is modeled by the following function:
2t+4
P(t) = 3
Complete the following sentence about the monthly rate of change in the number of people who receive
the email.
Round your answer to two decimal places.
Every month, the number of people who receive the email is multiplied by a factor of

Answer 1

Based on an exponential growth function, every month, the number of people who receive the email is multiplied by a factor of 10257.49.

An exponential growth function shows an increase in value occurring at a constant rate over time.

An exponential growth function is written as y = abˣ, and it is the opposite of an exponential decay function.

y = abˣ

The relationship between the elapsed time t, in months, since Venera sent the letter, and the number of people, P(t), who receive the email is modeled by the following function:

P(t) =
`2^((3t+7))`

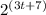
Every month, the number of people who receive the email is multiplied by a factor will be

For t = 2, we have:

P(2) =
`(2^(3t+7)) * ln(2) * 3`

=
`(2^13) * ln(2) * 3`

=
`(2^13) * ln(2) * 3`

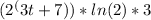
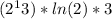
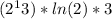
≈ 10257.49

Complete Question:

The relationship between the elapsed time t, in months, since Venera sent the letter, and the number of people, P(t), who receive the email is modeled by the following function:

P(t) =
`2^((3t+7))`

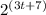
Complete the following sentence about the monthly rate of change in the number of people who receive

the email.

Round your answer to two decimal places.

Every month, the number of people who receive the email is multiplied by a factor of