Question

Assuming that sunlight produces , and the skin absorbs 50% of these photons (and reflects the other 50%) calculate the total UV energy absorbed over 0.42 m2 of skin that is exposed to sunlight for one hour. Assume that the average wavelength of the UV photons is 330 nm. (Hint: Be careful with units!)

Answer 1

The total UV energy absorbed over 0.42 m2 of skin that is exposed to sunlight for one hour is
`1.39 * 10^-^9`

How to determine this?

Sunlight arrives in the form of packets of energy known as photons.

To determine the energy of a single photon, you can use the equation:

`Energy \; of \; one \; photon = (hc)/(\Lambda)`

`= (6.6 * 10^-^3^4 Js * 3 *10^8ms^-^1 )/(330 * 10^-^9m)`

`=0.6 * 10^-^3^4J`

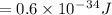
Skin absorbs 50% of photon, so number of photons absorbed by skin is:

`photons \; absorb = (3.066 * 10^2^2)/(2)`

`= 1.53 * 10^2^2 \;photons/m^2s`

Total energy calculation:

Total energy = energy of 1 photon × total photon × area × time

`0.6 * 10^-^3^4 J * 1.53 *10^2^2 \; photons /m^2s * 0.42m^2 * 3600s`

`=1388.02 * 10^-^1^2J`

`=1.39 * 10^-^9`

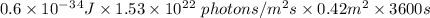
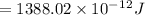
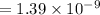
Therefore, the total UV energy absorbed over 0.42 m2 of skin that is exposed to sunlight for one hour is
`1.39 * 10^-^9`

Complete question:

Assuming that sunlight produces 3.066x10^22 UV Photons/m^2s

and that the skin absorbs one-half of these photons (and reflects the other half), calculate the total UV energy absorbed over 0.42 m^2 of skin that is exposed to sunlight for one hour. Assume that the average wavelength of the UV photons is 330 nm.