Falling object analysis: Height decreases, velocity becomes more negative (faster fall), initial height 0.29m, initial velocity -0.16m/s, acceleration -9.81m/s², both acceleration functions close to Earth's gravity, best fit captures constant acceleration.
The table shows the values of the position function and the velocity function for a falling object during an experiment. The position function gives the height of the object above the ground at a given time, and the velocity function gives the object's rate of change of height.
The table shows that the height of the object decreases as time increases. This is because the object is falling under the influence of gravity. The velocity of the object is also negative, which means that the object is falling downwards. The velocity of the object becomes more negative as time increases, which means that the object is falling faster and faster.
The initial height of the object is 0.290864 meters. The initial velocity of the object is -0.16405 meters per second. The acceleration of the object is -9.81 meters per second per second. This is equal to the acceleration due to gravity on Earth.
The velocity function can be found by taking the derivative of the position function. The acceleration function can be found by taking the derivative of the velocity function.
The table shows that the velocity function is a good fit for the data given in the table. This is because the velocity function is able to capture the trend of the data, which is that the velocity of the object is becoming more negative as time increases.
The velocity function found in Exercise 1 is
 The velocity function found in Exercise 3 is
The velocity function found in Exercise 3 is
 The acceleration function found in Exercise 1 is
The acceleration function found in Exercise 1 is
 The acceleration function found in Exercise 3 is
The acceleration function found in Exercise 3 is

Both of the acceleration functions are close to the acceleration due to gravity on Earth, which is -9.81 meters per second per second. However, the acceleration function found in Exercise 3 is a better fit for the data given in the table. This is because the acceleration function found in Exercise 3 is able to capture the trend of the data, which is that the acceleration of the object is constant.
The position function of another free-falling object is given by

To find
 we need to take the derivative of
we need to take the derivative of
 .
.
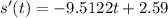
We can use
 to determine the maximum height of the object by finding the time at which
to determine the maximum height of the object by finding the time at which
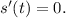
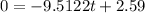
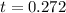
The maximum height of the object is s(0.272).
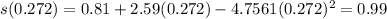
The velocity of the object at this time is
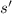
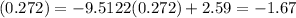
 is positive when -0.272 < t < 0.057.
is positive when -0.272 < t < 0.057.
 is negative when t < -0.272 or t > 0.057. This means that the object is falling when t < -0.272 or t > 0.057, and the object is rising when -0.272 < t < 0.057.
is negative when t < -0.272 or t > 0.057. This means that the object is falling when t < -0.272 or t > 0.057, and the object is rising when -0.272 < t < 0.057.