Yes, you can solve a system of linear equations by substitution. In the context of the provided graph and equations, the point of intersection (4, 5) indicates the solution to the system of equations y = x + 1 and
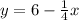 .
.
Yes, you can solve a system of linear equations by substitution. In the context of the provided graph and equations, the point of intersection (4, 5) indicates the solution to the system of equations y = x + 1 and
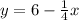 .
.
To solve the system by substitution, you would set the expressions for
 equal to each other:
equal to each other:
![\[ x + 1 = 6 - (1)/(4)x \]](https://img.qammunity.org/2024/formulas/mathematics/college/7rp0kgc4gxeh8gsyjeoox3p55gh4sujkz8.png)
Then, you would solve for
 :
:
![\[ x + (1)/(4)x = 6 - 1 \]](https://img.qammunity.org/2024/formulas/mathematics/college/horencshd4t88fczkq1968x3902cbpk53u.png)
Combine like terms:
![\[ (5)/(4)x = 5 \]](https://img.qammunity.org/2024/formulas/mathematics/college/xc7cl6ekl90bzr41ec6t2p0whwakixut65.png)
Solve for
 :
:
![\[ x = 4 \]](https://img.qammunity.org/2024/formulas/mathematics/college/dbr8h0mpfbke3yr58meypye7rkg6o448t2.png)
Now that you have the value of
 , substitute it back into one of the original equations to find
, substitute it back into one of the original equations to find
 . Using the first equation
. Using the first equation
 :
:
![\[ y = 4 + 1 = 5 \]](https://img.qammunity.org/2024/formulas/mathematics/college/ye90ei4idpbuaffsrj4g2d3tk0mnh9k3vr.png)
So, the solution to the system of equations is
 , which matches the given point of intersection (4, 5) on the graph. This confirms that the point (4, 5) is a valid solution to the system of equations.
, which matches the given point of intersection (4, 5) on the graph. This confirms that the point (4, 5) is a valid solution to the system of equations.