Question

How many cubes with edge length 1/5 inch fit in the prism of 15.36.

Answer 1

1920 cubes with an edge length of 1/5 inch each fit in the prism with a total volume of 15.36 cubic inches.

To determine the number of cubes with an edge length of 1/5 inch that fit in a prism of volume 15.36 cubic inches, we can use the formula for the volume of a prism:
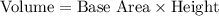`\(\text{Volume} = \text{Base Area} * \text{Height}\)`. In this case, the base area is each face of the cube, and the height is the number of cubes stacked.

The volume of one cube is given by
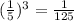`\(((1)/(5))^3 = (1)/(125)\)` cubic inches. To find the number of cubes that fit, divide the total volume of the prism by the volume of one cube:

`\[ \text{Number of Cubes} = \frac{\text{Total Volume}}{\text{Volume of One Cube}} \]`

`\[ \text{Number of Cubes} = (15.36)/((1)/(125)) \]`

`\[ \text{Number of Cubes} = 15.36 * 125 \]`

`\[ \text{Number of Cubes} = 1920 \]`

Therefore, 1920 cubes with an edge length of 1/5 inch each fit in the prism with a total volume of 15.36 cubic inches.