Answer:
9 pitchers
Explanation:
Given
Cylinder 1:
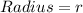
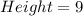
Cylinder 2:
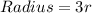
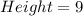
Required
How many pitchers' cylinder 2 can fill
First, we calculate the volume of both cylinders
Volume is calculated as:
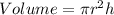
For A:
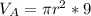
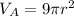
For B:
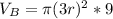
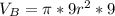
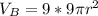
In (a):
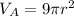
So, we have ve:
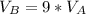
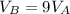
If the first cylinder can fill 1, then the second can fill 9 pitchers