There isn't sufficient evidence at the 5% significance level to conclude that the customer satisfaction rate is higher than the claimed rate of 62%.
To determine if there's sufficient evidence that the customer satisfaction rate is higher than the claimed 62%, you can conduct a hypothesis test for the proportion.
Given:
Current claimed satisfaction rate by the company (null hypothesis):
p_0 =0.62
Sample size:
n=145
Number of satisfied customers in the sample:
Satisfied=96
Step 1: Formulate Hypotheses
Null Hypothesis (H_0 ): The customer satisfaction rate is the same as claimed (p≤p_0 ).
Alternative Hypothesis (H_1 ): The customer satisfaction rate is higher than claimed (p>p_0).
Step 2: Calculate the Test Statistic (z-score)
The formula for the z-score for testing a proportion is:
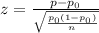
Where:
p is the sample proportion (Satisfied n Satisfied
p_0 is the claimed proportion
n is the sample size
Substituting the values:
p= 96/145= 0.6621
z≈ 0.0421/ 0.62⋅0.38/ √145
z≈ 0.0421/ 0.0474
z≈0.887
Step 3: Find the p-value
To find the p-value, we'll use the z-score of 0.887 and a one-tailed test since we're testing if the satisfaction rate is higher than claimed.
From a standard normal distribution table or using statistical software, the p-value corresponding to z=0.887 is approximately 0.1887.
Step 4: Make a Decision
At a significance level of α=0.05, since the p-value (0.1887) is greater than the significance level, we fail to reject the null hypothesis.