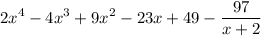Question

Efectúa la siguiente division aplicando la regla de ruffini (2x⁵ - 3x³ + 4x³ - 5x² + 3x + 1) (x + 2)​

Answer 1

`\displaystyle 2x^4-4x^3+9x^2-23x+49-(97)/(x+2)`

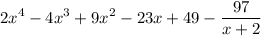
Explanation:

Ruffini's rule, commonly known as synthetic division, is a method of dividing polynomials by a linear factor.

First, we will find a linear factor to divide by. We will do this by using the root associated with the divisor. ((x + 2) ➜ -2)

Next, we list out the coefficients of the dividend.

We bring the first number down and multiply by our factor (-2). Then we move this number underneath the number in the next column, add, multiply, and repeat. See attached for this process.

Next, starting with a degree below the dividend (5 - 1 = 4), we write out using these numbers as coefficients. The remaining -97 is our reminder.

`\displaystyle 2x^4-4x^3+9x^2-23x+49-(97)/(x+2)`