Question

T varies directly as the square of P and inversely as Z and T=12 when P=3 and Z=6

5. Using k as the constant of variation, which of the following is the equation of variation?
A. T=
\frac{kp {}^{2} }{z}
z
kp
2

​

B. T=
kpz {}^{2}kpz
2

C. T=
\frac{kz}{p {}^{2} }
p
2

kz
​

D. T=
\frac{pz {}^{2} }{k}
k
pz
2

​


6. Which of the following is the value of the variation constant:
A. 6
B. 8
C. 10
D. 12

7. Which of the following is twice the value of T when P=9 and Z=6?
A. 108
B. 216
C. 54
D. 36
​

Answer 1

A.
`T= (KP^2)/(Z)`

D. K = 8

B. 216

Explanation:

Q. T varies directly as the square of P and inversely as Z and T=12 when P=3 and Z=6

Solution:

According to the given information:

T varies directly as the square of P.

`T\alpha P^2..... (1)`

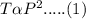
T varies inversely as Z.

`T\alpha (1)/(Z) ..... (2)`

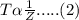
Combining equations (1) & (2)

`T\alpha (P^2)/(Z)`

`T= (KP^2)/(Z)`

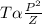
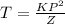
(Where K is proportionality constant)

(This is the equation of variation)

Plug T=12, P=3 and Z=6 in the above equation of variation, we find:

`12= (K(3)^2)/(6)`

`12= (K* 9)/(6)`

`K= (12* 6)/(9)`

`K= (72)/(9)`

`K= 8`

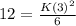
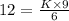
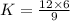
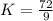
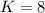
So, the value of the variation constant = 8

Next, plug P=9, Z=6 and K = 8 in the above equation of variation, we find:

`T= (8(9)^2)/(6)`

`T= (8* 81)/(6)`

`T= (648)/(6)`

`T= 108`

`2T= 2* 108`

`2T= 216`

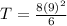
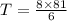
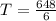
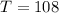
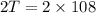
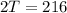
So, 216 is twice the value of T.