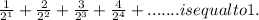Question

Evaluate the sum 1/2^1 + 2/2^2…

Answer 1

The sum of the given series
`(1)/(2^1) + (2)/(2^2) +(3)/(2^3) + (4)/(2^4) + ....... is equal to 1.`

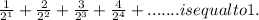
The sum you've provided is an example of an infinite geometric series. The general form of an infinite geometric series is given by:

S = a + ar + ar² + ar³ +...

where a is the first term and r is the common ratio.

In your case, the series is:

S=++++...

Here, a= 1/2 and r = 1/2

The sum of an infinite geometric series is given by the formula:

S = a/1-r

Substituting the values, we get:

S= 1/2 /1- 1/2

Simplifying this expression:

`S=((1)/(2) )/((1)/(2) )`

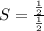
Canceling out the common factor of
`(1)/(2)` , we get:

S=1

Therefore, the sum of the given series
`(1)/(2^1) + (2)/(2^2) +(3)/(2^3) + (4)/(2^4) + ....... is equal to 1.`