Question

Please explain this problem!!!​

Answer 1

tis a little of plain differentiation.

we know the radius of the cone is decreasing at 10 mtr/mins, or namely dr/dt = -10, decreasing, meaning is negative.

we know the volume is decreasing at a rate of 1346 mtr/mins or namely dV/dt = -1346, also negative.

so, when h = 9 and V = 307, what is dh/dt in essence.

we'll be needing the "r" value at that instant, so let's get it

`V=\cfrac{1}{3}\pi r^2 h\implies 307=\cfrac{\pi }{3}r^2(9)\implies \sqrt{\cfrac{307}{3\pi }}=r`

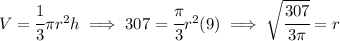
now let's get the derivative of the volume of the cone

`V=\cfrac{1}{3}\pi r^2 h\implies \cfrac{dV}{dt}=\cfrac{\pi }{3}\stackrel{product~rule}{ \left[ \underset{chain~rule}{2r\cdot \cfrac{dr}{dt}}\cdot h+r^2\cdot \cfrac{dh}{dt} \right]} \\\\\\ -1346=\cfrac{\pi }{3}\left[2\sqrt{\cfrac{307}{3\pi }}(-10)(9)~~+ ~~ \cfrac{307}{3\pi } \cdot \cfrac{dh}{dt}\right]`

`-\cfrac{4038}{\pi }=-\cfrac{180√(307)}{√(3\pi )}+\cfrac{307}{3\pi } \cdot \cfrac{dh}{dt}\implies \left[ -\cfrac{4038}{\pi }+\cfrac{180√(307)}{√(3\pi )} \right]\cfrac{3\pi }{307}=\cfrac{dh}{dt} \\\\\\ -\cfrac{12114}{307}+\cfrac{180√(3\pi )}{√(307)}=\cfrac{dh}{dt}\implies -7.920939735970634 \approx \cfrac{dh}{dt}`