Question

`f(x)=(1-0.08)^{(1)/(12) } ^((12t))`

my teacher then said from that you get
`f(x)=(0.993)^(12t)`


can someone explain how you get to this? Please explain this to me I am so confused?

Answer 1

See Below.

Explanation:

We have:

`\displaystyle f(x)=(1-0.08)^{(1)/(12)(12t)}`

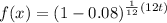
First, we can subtract within the parentheses:

`f(x)=(0.92)^{(1)/(12)(12t)}`

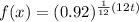
By the properties of exponents:

`f(x)=((0.92)^(1)/(12))^(12t)`

Approximate. Use a calculator:

`f(x)\approx (0.993)^(12t)`

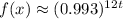
Notes:

0.993 is only an approximation, hence the approximately equal sign.

I'm not given the context of the problem, but it's simpler to just simplify in the exponent like so (the fractions cancel):

`\displaystyle f(x)=(1-0.08)^{(1)/(12)(12t)}=(0.92)^t`

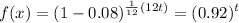
Full Problem:

The value of Sara's car decreases at a rate of 8% per year.

We will use the exponential decay formula with a set time, given by:

`f(x)=a(r)^(x/d)`

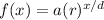
Where a is the initial value, r is the rate, x is the time that has passed (dependent on d), and d is the amount of time for one decrease.

For this problem, we can ignore the initial value.

And since the value decreases at a rate of 8% per year, r = 0.92 (we acquire this from 1 - 0.08).

Part 1) Per Month:

Since it decreases per month, d = 12.

`f(x)=(0.92)^(x/12)`

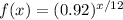
Approximate:

`f(x)=((0.92)^(1/12))^x\approx(.993)^x`

In this case, x is measured in months.

Part 2) Per Week:

Since it decreases per week, d = 52.

`f(x)=(0.92)^(x/52)`

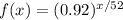
Approximate:

`f(x)=((0.92)^1/52)^x\approx (.998)^x`

In this case, x is measured in weeks.

Part 3) Per Day:

So, d = 365.

`f(x)=(0.92)^(x/365)`

Simplify:

`f(x)=((0.92)^(1/365))^x\approx(.999)^x`

In this case, x is measured in days.

Part 4)

So, as d increases, our r increases as well.

Therefore, the smaller the time interval (from months to weeks to days), the higher our rate of decrease is.