The equation of the circle with center at the origin is

Let's denote the center of the circle as
 and the point of tangency with one of the tangents as
and the point of tangency with one of the tangents as
 . The angle between the two tangents is formed by the radii from the center
. The angle between the two tangents is formed by the radii from the center
 to the points of tangency
to the points of tangency
 where
where
 is the point of tangency with the second tangent. The angle between the two tangents is 46 degrees.
is the point of tangency with the second tangent. The angle between the two tangents is 46 degrees.
The radius at the point of tangency is perpendicular to the tangent. Therefore, the angle
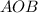 is a right angle. Since the angle between the tangents is given as 46 degrees, the angle
is a right angle. Since the angle between the tangents is given as 46 degrees, the angle
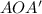 (where
(where
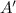 is the reflection of
is the reflection of
 across the x-axis) is
across the x-axis) is
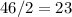 degrees.
degrees.
Now, we have a right-angled triangle
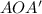 where we know the angle
where we know the angle
 degrees and the coordinates of
degrees and the coordinates of
 . Using trigonometry, we can find the length of \(OA\) (the radius) and then use it to find the equation of the circle.
. Using trigonometry, we can find the length of \(OA\) (the radius) and then use it to find the equation of the circle.
Let
 be the radius, then:
be the radius, then:
![\[ \tan(23^\circ) = (OA')/(OA) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/n511wp9lyk2fvrf18fx87w1umqdi9clr7v.png)
![\[ \tan(23^\circ) = (0 - r)/(13) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xd7m8woe98660nq18kftt1obufdr7k2x7a.png)
Solving for
 , we get:
, we get:
![\[ r = -13\tan(23^\circ) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vkd9i4hvx0w5m2z6ib6i74g1h8nfl6jb7h.png)
Now, the equation of the circle with center
 is given by:
is given by:
![\[ (x - h)^2 + (y - k)^2 = r^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/y5087c6sod0r2ikyfgb9t9j0fjw17zohhe.png)
Substitute
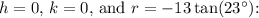
![\[ x^2 + y^2 = (-13\tan(23^\circ))^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8v4sh8nm8txhwx0wo66c5ph8y4l2sts9gp.png)
Simplify the equation:
![\[ x^2 + y^2 = 169\tan^2(23^\circ) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/55y80so50mmkffo40zd2mwj0jojjgrhyi0.png)
So, the correct equation of the circle with center at the origin
 and radius
and radius
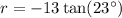 is:
is:
![\[ x^2 + y^2 = 169\tan^2(23^\circ) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/55y80so50mmkffo40zd2mwj0jojjgrhyi0.png)