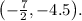The y-intercept is at (0, 20).
The vertex of the quadratic function
 is
is
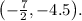
To identify the x-intercepts, y-intercept, and vertex of the quadratic function
 , let's break down each component:
, let's break down each component:
1. **X-intercepts:**
X-intercepts occur where the graph intersects the x-axis, i.e., where y = 0. To find them, set y to 0 and solve for x:
![\[ 2x^2 + 14x + 20 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/s1fu62mv5sewuygsnzviq4ywlfo3t4lpp0.png)
You can use the quadratic formula to solve for
 , which is
, which is
 in this case.
in this case.
2. **Y-intercept:**
The y-intercept is where the graph intersects the y-axis, and for any function, it occurs when x = 0. Substituting x = 0 into the function gives the y-intercept:
![\[ y = 2(0)^2 + 14(0) + 20 = 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/v0j7vkedbne8s96e8dxqf8b1qew04wpytu.png)
3. **Vertex:**
The vertex of a quadratic function in the form
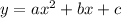 is given by the coordinates
is given by the coordinates
 , the x-coordinate of the vertex is
, the x-coordinate of the vertex is
 , and substituting this into the function gives the y-coordinate:
, and substituting this into the function gives the y-coordinate:
![\[ y = 2\left(-(7)/(2)\right)^2 + 14\left(-(7)/(2)\right) + 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bdob5i8ji58yb2csgaiz0y8hsv94i3aewu.png)
simplify the expression step by step:
![\[ y = 2\left(-(7)/(2)\right)^2 + 14\left(-(7)/(2)\right) + 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bdob5i8ji58yb2csgaiz0y8hsv94i3aewu.png)
1. Square the term inside the parentheses:
![\[ = 2 * (49)/(4) + 14\left(-(7)/(2)\right) + 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vwbo88toqaeeqp4vkweoe5p4r57x5r0lfo.png)
2. Multiply 2 by \(\frac{49}{4}\):
![\[ = (98)/(4) + 14\left(-(7)/(2)\right) + 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jc9dlgb6o5bmys9slync51zoutaoyj3b13.png)
3. Simplify the fraction:
![\[ = 24.5 - 49 + 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/krryh7dybmm7r3t8hl20xaf8enk7dpkbpi.png)
4. Combine like terms:
![\[ = -4.5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/c9abomlmvmi3brxvta159fl8t5w8gsozej.png)
Therefore, the y-coordinate of the vertex is -4.5.
So, the simplified expression is:
![\[ y = -4.5 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5iim37xaonpbocpk4abo6iykzm3l0q15tl.png)
The vertex of the quadratic function
 is
is