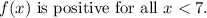
The function
 can be analyzed to determine its behavior across different ranges of x-values. To find where the function is positive or negative, it's essential to examine its factors and critical points.
can be analyzed to determine its behavior across different ranges of x-values. To find where the function is positive or negative, it's essential to examine its factors and critical points.
Firstly, let's factor the denominator of the function to understand its behavior. The denominator
 factors to
factors to
 This means the function has vertical asymptotes at
This means the function has vertical asymptotes at
 and
and
 .
.
Now, consider the signs of the function in the intervals created by these critical points. When
 , both the numerator and denominator are negative, resulting in a positive
, both the numerator and denominator are negative, resulting in a positive
 (negative divided by negative equals positive). Between
(negative divided by negative equals positive). Between
 , the numerator is positive while the denominator remains negative, making
, the numerator is positive while the denominator remains negative, making
 negative (positive divided by negative equals negative). Finally, for
negative (positive divided by negative equals negative). Finally, for
 , both the numerator and denominator are positive, leading to a positive
, both the numerator and denominator are positive, leading to a positive
 (positive divided by positive equals positive).
(positive divided by positive equals positive).
Given the options provided,
 is positive for all ( x < 7 ). Therefore, the correct statement among the options is "f(x) is positive for all x < 7".
is positive for all ( x < 7 ). Therefore, the correct statement among the options is "f(x) is positive for all x < 7".