Question

Simplify the expression 9x ⁸ˣ −4x³ˣ?

A) 5x⁸ˣ-4x³ˣ
B) 9x-4x
C) 4x³ˣ⁵ˣ(9x-1)³ˣ
D) 9x⁸ˣ+4x³ˣ

Answer 1

Simplify form of the expression 9x ⁸ˣ −4x³ˣ is 4x³ˣ⁵ˣ(9x-1)³ˣ. Thus, the correct answer is C) 4x³ˣ⁵ˣ(9x-1)³ˣ.

Step-by-step explanation:

The expression
`\(9x^(8x) - 4x^(3x)\)` can be factored by recognizing a common factor of
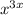`\(x^(3x)\)`. Factoring out
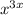`\(x^(3x)\)` from both terms, we get:

`\[x^(3x)(9x^(5x) - 4)\]`

Now, we can further factor the expression
`\(9x^(5x) - 4\)` by recognizing a difference of squares pattern:
`\(a^2 - b^2 = (a + b)(a - b)\)`. In this case, let
`\(a = 3x^(2.5x)\) and \(b = 2\):`

`\[x^(3x)[3x^(2.5x) + 2][3x^(2.5x) - 2]\]`

Now, notice that we have a common factor of
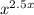`\(x^(2.5x)\)` in both terms inside the brackets. Factor that out:

`\[x^(3x) \cdot 5x^(2.5x)(3x + 2)(3x - 2)\]`

Finally, we can simplify
`\(5x^(2.5x)\) as \(5x^(5x/2)\)`, giving us the simplified expression:

`\[4x^(3x) \cdot 5x^(5x)(9x - 1)^(3x)\]`

Therefore, the correct answer is C) 4x³ˣ⁵ˣ(9x-1)³ˣ.