When a metal block is weighed in water, the buoyant force equals its weight at equilibrium. Using Archimedes' principle, the volume of the metal block is calculated, and its density is determined as the ratio of its mass to the calculated volume.
a) Free-Body Force Diagrams:
1. In Air:
- Weight
 downward.
downward.
- Tension
 upward (assuming it's held in place).
upward (assuming it's held in place).
- No buoyant force in air.
2. In Water:
- Weight
 downward.
downward.
- Buoyant force
 upward.
upward.
- Tension
 upward (assuming it's held in place).
upward (assuming it's held in place).
b) Force Equation at Equilibrium in Water:
- At equilibrium, the block is not accelerating, so the net force is zero.
-

-
 (since
(since
 is canceled out by
is canceled out by
 in the opposite direction).
in the opposite direction).
-
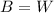
-
 (where
(where
 is the acceleration due to gravity, approximately
is the acceleration due to gravity, approximately
 .
.
c) Archimedes' Principle:
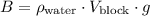
- Archimedes' principle states that the buoyant force
 is equal to the weight of the fluid displaced by the object.
is equal to the weight of the fluid displaced by the object.
-
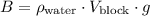
- Since B=W (at equilibrium),
 .
.
- Solving for
 .
.
d) Determine Density of the Metal Block:
- Density
 is given by
is given by
 .
.
- Substituting the expression for
 from part (c):
from part (c):
 .
.
- Simplifying:
 =
=
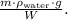
Given the values of
 (mass in air) and
(mass in air) and
 (apparent mass in water), and knowing
(apparent mass in water), and knowing
 and the density of water
and the density of water
 , you can calculate the density of the metal block using the final expression obtained in part (d).
, you can calculate the density of the metal block using the final expression obtained in part (d).