Question

Find the composite functions f(g(x)) and g(f(x)) for the given functions (x)=2x3³and g(x)=3x.

Answer 1

The composite functions f(g(x)) and g(f(x)) for the given functions (x)=2x3³and g(x)=3x are
`\[ f(g(x)) = 18x^3 \quad \text{and} \quad g(f(x)) = 54x^9 \]`

Step-by-step explanation:

In the composite function f(g(x)), you substitute the expression for g(x) into f(x), yielding f(g(x)) =
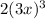`2(3x)^3`. Simplifying, you get f(g(x)) =
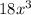`18x^3`. Conversely, for g(f(x)), you substitute f(x) into g(x), resulting in g(f(x)) =
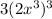`3(2x^3)^3`, which simplifies to g(f(x)) =
`54x^9.`

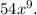
The first composite function,
`\( f(g(x)) = 18x^3 \)`, represents the cube of three times the input, while the second composite function,
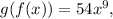`\( g(f(x)) = 54x^9 \),` signifies the ninth power of twice the input.

These composite functions demonstrate the transformative nature of function composition, where the output of one function becomes the input for the other.