Question

Solve for y in
12y′−6y=0,given y(0)=50."

Answer 1

The solution for y in the given differential equation 12y' - 6y = 0, with the initial condition y(0) = 50, is y = 50 *
`e^(^1^/^2^*^x^)`.

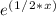Step-by-step explanation:

The provided differential equation is a first-order linear ordinary differential equation, and its solution involves separating variables and integrating. The solution to this specific equation is a function of the form y = C *
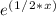`e^(^1^/^2^*^x^)`, where C is the constant of integration. To determine the value of C, the initial condition y(0) = 50 is used.

The solution process involves integrating the given equation, leading to the expression y = C *
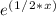`e^(^1^/^2^*^x^)`. Applying the initial condition, y(0) = 50, allows us to solve for C and obtain the specific solution for this problem. In this case, C turns out to be 50, resulting in the final solution y = 50 * e^(1/2*x).

The exponential term in the solution reflects the growth or decay behavior of the function. In this context, the base of the exponential function,
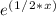`e^(^1^/^2^*^x^)`, indicates a growth rate proportional to the square root of x. Thus, the solution represents a curve that grows gradually as x increases.

In summary, the solution to the differential equation 12y' - 6y = 0, with the initial condition y(0) = 50, is y = 50 *
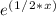`e^(^1^/^2^*^x^)`.