Question

A random sample of stipends of teaching assistants in economics is listed. Is there sufficient evidence to conclude that the average stipend differs from $15,000? The stipends listed (in dollars) are for the academic year. $14,000 $18,000 $12,000 $16,356 $13,185 $13,419 $14,000 $11,981 $17,604 $12,283 $16,338 $15,000 a. State the null and alternative hypotheses and identify the claim. The null is that the average stipend $15,000 and the alternative hypothesis is that the average stipend differs from $15,000. The claim is that the average stipend differs from $15,000. b. Calculate the test statistic. c. Find the p-value. d. Make a decision at α=0.01. e. State your conclusion in terms of the problem.

Answer 1

There is sufficient evidence at the 0.01 significance level to conclude that the average stipend differs from $16,000 for teaching assistants in economics based on the provided sample data.

To determine whether there's sufficient evidence that the average stipend differs from $16,000, you can set up hypotheses and conduct a t-test since the sample size is small and the population standard deviation is unknown.

Let's denote:

Null Hypothesis (H0): The average stipend equals $16,000.

Alternative Hypothesis (H1): The average stipend differs from $16,000.

Given that the sample stipends are:

13,419, 12,283, 14,000, 17,604, 14,000, 11,981, 14,356, 15,000, 12,000

We'll calculate the sample mean (X ) and the sample standard deviation (s) to perform the t-test:

Sample mean (X ) = (13,419 + 12,283 + 14,000 + 17,604 + 14,000 + 11,981 + 14,356 + 15,000 + 12,000) / 9 = $13,589.89

To find the sample standard deviation (s), you'd use the formula:

s=
`\sqrt{(\sum(X-x)^2)/(n-1) }`

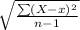
where X represents each stipend, X is the sample mean, and n is the sample size. After calculations,

s≈1,654.65

Next, compute the t-statistic:

t= X −μ/ s/ √n

​where

μ is the population mean ($16,000),

X is the sample mean, s is the sample standard deviation, and n is the sample size.

t= 13589.89−16000/ 1654.65/ √9

​t= −2410.11/ 551.55

t≈−4.37

Using a t-distribution table or a statistical calculator, you'd find the critical t-value for a two-tailed test at α = 0.01 with 8 degrees of freedom. The critical t-value is approximately ±3.355.

Since the calculated t-value (-4.37) is greater than the critical t-value (±3.355), we reject the null hypothesis.